ハノイの塔
ハノイの塔の伝説
今から5000年まえ,インドのベナレスという町に大寺院があり,そこには世界の中心といわれるドームがありました。その中には台が作られていて,その上にはダイヤモンドでできた棒が3本立っていました。インドの神ブラーマは,世界が始まるときに,この棒に黄金でできた円盤を64枚さしておきました。この円盤は下が大きく,上に行くほど小さくできていて,ピラミッド状に積み上げられていました。そして,ブラーマは僧侶たちに次のような修行を与えました。
- 積み上げられた円盤を,すべて他の棒に移すこと。
- その際に,1回に1枚しか動かしてはならない。また,小さな円盤の上にそれより大きな円盤を乗せてはならない。
- すべてこの3本の棒を使って移すこと。棒以外のところに円盤を置いてはならない。
ブラーマは,この円盤がすっかり他の棒に移った瞬間に,世界は消滅してしまうと予言しています。5000年たった今でも,寺院ではこの修行が続けられているそうなのですが・・・
 模型による実験
模型による実験
3枚の円盤で行うと,最低7回でできます。右の写真は4枚ですが,円盤4枚だと最低15回になります。円盤の枚数が1枚ずつふえると,回数がどのくらいずつふえていくのでしょうか。円盤が3枚や4枚くらいだと,わが家の子供でも5分もかからずにできてしまいます。
こども 「円盤が64枚だったら,数時間でできるんじゃない?」
父さん 「だったら,もうとっくに世界は消滅してるじゃないかぁ〜」
こども 「だからぁ〜,そんな伝説はウソウソ!」
父さん 「まてよぉ〜? 彦一の有名な米粒の話もあるしなぁ・・・」
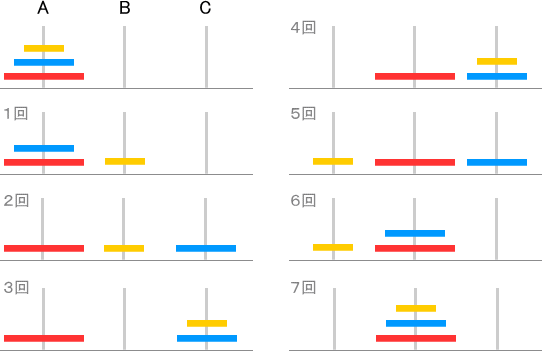
その後,子供は訓練して,5枚を約30秒で動かせるようになりました。コツを発見したそうで,AからBへ移しかえる場合は,円盤が奇数枚なら1枚目をBに移し,偶数枚ならCに移すことだそうです。
計算をしました
じつを言うと,この問題は数学の「数列」という分野でとり上げられる,有名なパズルなのです。円盤の枚数と移動回数の関係は,以下のようになることが知られています。
円盤の枚数を n とすると,移動回数は 2n-1 (2の n 乗−1)
表計算ソフトで計算してみると,次のようになりました。かりに,むだなく円盤を正確に移動できたとして,1枚を動かすのに1秒かかったとします。それでも64枚を動かすのに,不眠不休でやっても5800億年かかってしまいます。
| 枚数 |
移動回数 |
所要時間 |
| 3 |
7 |
7秒 |
| 4 |
15 |
15秒 |
| 5 |
31 |
31秒 |
| 6 |
63 |
1分3秒 |
| 7 |
127 |
2分7秒 |
| 8 |
255 |
3分15秒 |
| 9 |
511 |
6分31秒 |
| 10 |
1023 |
17分3秒 |
| 11 |
2047 |
34分7秒 |
| 12 |
4095 |
1時間8分15秒 |
| 13 |
8191 |
2時間16分31秒 |
| 14 |
16383 |
4時間33分3秒 |
| 15 |
32767 |
9時間6分7秒 |
|
| 枚数 |
移動回数 |
所要時間 |
| 18 |
262143 |
3日49分3秒 |
| 24 |
16777215 |
194日4時間20分15秒 |
| 25 |
33554431 |
1年23日8時間40分31秒 |
| 26 |
約6700万 |
約2年 |
| 30 |
約11億 |
約34年 |
| 32 |
約43億 |
約136年 |
| 35 |
約340億 |
約1000年 |
| 40 |
約1兆1000億 |
約35000年 |
| 45 |
約35兆2000億 |
約110万年 |
| 50 |
約1100兆 |
約3600万年 |
| 55 |
約36に0が15個 |
約11億年 |
| 62 |
約46に0が17個 |
約1500億年 |
| 64 |
約18に0が18個 |
約5800億年 |
|
宇宙の始まりのビッグバンは,約150億年まえだと言われています。地球に生命の祖先が生まれたのが,約40億年まえです。5800億年という時間のすごさが,分かるような気が・・・う〜ん,やっぱり実感できないなぁ。
(^^);
ハノイの塔は,1883年にフランスのE.リュカ教授が考案したパズルです。伝説も,教授が書かれた本にあるそうです。
とんち彦一ばなし (彦一どんと殿さん)
とんちで有名な彦一が,八代(熊本県)の殿さまから,ほうびをもらうことになりました。
「彦一,何でんよか,おまえの好きなもんをほうびにやるから,申せ。」
「いやぁ,たいしたこつぁしとらんですけん,いりまっせんバイ。」
「何ば言うか,やると言うとるんだから,何でんよか,申せ。」
「殿さん,本当に何でんよかとですか?」
「くどか! 俺は殿さんゾ,何でんできるから,申せ!」
そこで,彦一が言うには,
「殿さんは,将棋が好きですね。将棋盤の最初の”ます目”に米を1粒置いてください。
2番目の”ます目”には2粒,3番目には4粒,4番目には8粒,・・・・・というふうに,
将棋盤の最後の”ます”まで米粒を置いていき,将棋盤全体の米粒をもらおうごたっとバッテン,
よかですか?」
「なんや,そんくらいか。彦一は欲んなかな。よかバイ。持ってけ,持ってけ。」
「ほんなこつ,よかですか? そんなら証文ば書いてくだはりまっせ。」
殿さまは,「将棋盤の各々のますに,次々と倍々にして置いていく米粒を彦一に与える」
という約束を文書にして渡しました。
さて,殿さまは約束を守ることができたのでしょうか?この米粒の量は,いったいどれだけになるのでしょう?
計算すると。
1+2+4+8+16+32+64+128+・・・・
将棋盤のます目は81(9×9)だから,
初項が1,公比が2の等比数列の,初項から第81項までの和となります。
よって,等比数列の和の公式を使えば 281−1 (2の81乗−1) となります。
この数値は,おおざっぱに見積もっても 24×1023 粒です。
さて,日本の米の年間生産量は約1000万トンです。米は50粒で約1gですから,これは,日本全国の生産量の約50億年分に相当します。お父さんは,実際に米粒の重さを量って,計算したんだぞぉ〜,信じてくれぇ・・・

 模型による実験
模型による実験