三角形の面積

小学４年生では長方形や正方形の面積の求め方を学習します。ところで，お父さんは先走って「三角形の面積は長方形の半分だから，ついでに勉強しとけばぁ？」と子供に言ってしまいました。しかし考えてみると，そう簡単ではないことに気づきました。そこで，ちょっと面白半分に職場の同僚たちに次のような問題を出してみることにしました。

（問題）
底辺の長さが一定で，同じ高さの三角形はどのような形であっても同じ面積になることを説明しなさい。ただし，小学４年生にも理由が実感できるようにすること。

以下の説明は職場の大人たちが苦心して（仕事より面白いと言ってた人もいました）考えたものです。この考え方は他の場面でも応用できそうですね。

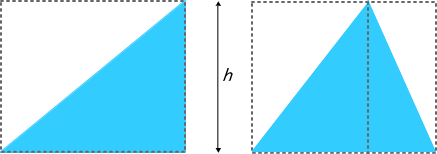
周知のように，三角形の面積は「底辺（長さ）と高さの積の半分」です。下の図１で，三角形はそれを囲む長方形の面積の半分になることが容易に理解できます。つまり，長方形や正方形の中に含まれる三角形は「三角形の面積は長方形や正方形の面積の半分になる」ことが直感的に分かりやすいのです。

（図１）

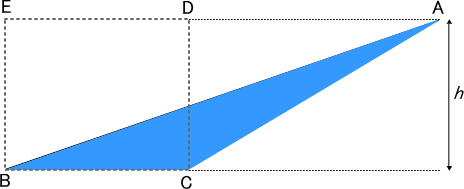
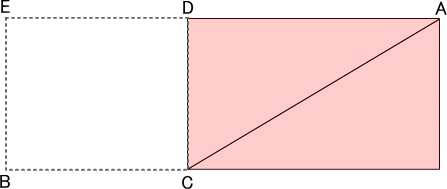
では，図１と同じ長さの底辺と高さをもった三角形で，図２のような三角形ABCはどうでしょうか？

（図２）

まず，三角形ABCの２倍の面積をもった平行四辺形AFBCを作ります。目的は，平行四辺形AFBCは長方形DEBCと同じ面積になることの説明です。

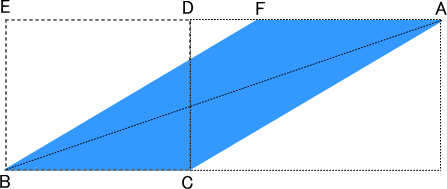
つぎに，三角形FEBを矢印のように移動します。

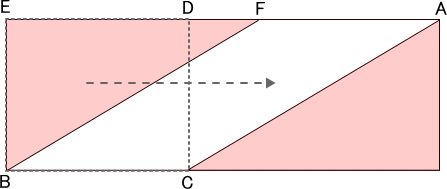
すると，平行四辺形AFBCの面積ぶんだけ長方形DEBCの面積ができます。すなわち，両者は同じ面積であることが分かります。

平成１５年に５年生になった長男は以下のように答えました。

底辺の長さと，高さがそれぞれ等しい平行四辺形は，形がちがっていても面積は等しい。そして，平行四辺形は長方形になおして面積を考えることができる。

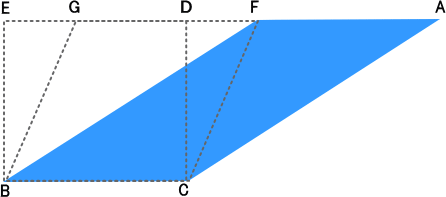
三角形AFCを三角形FGBの場所にうつす。つぎに，三角形FDCを三角形GEBの場所にうつす。したがって，平行四辺形AFBCと長方形DEBCの面積は等しい。
平行四辺形AFBC，平行四辺形FGBC，長方形DEBC，それぞれの面積の半分が三角形の面積になる。

台形の面積

現在の小学５年生は，台形の面積をもとめる公式を教科書で習いません。でも，今までに習ったことをもとにして，くふうしてみると公式を出すことができます。公式だけは知っていても，どのようにしてその公式ができたか，説明できない大人はたくさんいます。じつは，うちのお父さんも今までそうでしたぁ　(^^ゞ

その１　台形を２倍にして平行四辺形を作り，その半分の面積と考える。

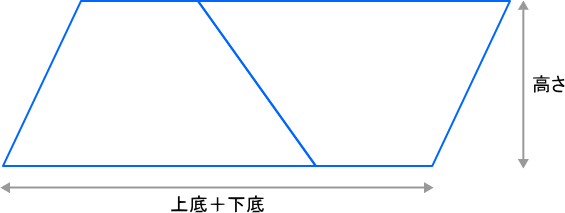
これですんなり，台形の面積をもとめる公式が　　となるのが分かりますね。

その２　台形を２つの三角形に分けて，それぞれの三角形の面積をもとめて合計する。

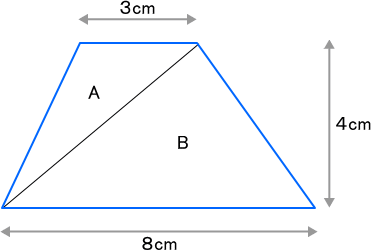
これも台形の面積をもとめる公式と同じになりました。